Ein Umfüllproblem
Miniwelt "Eimer umfüllen"
Zum Nudelkochen im Ferienlager werden genau 2 Liter Wasser benötigt. Zum Abmessen stehen nur ein kleiner Eimer, der 3 Liter fasst, und einen etwas größerer Eimer, der 4 Liter fasst, zur Verfügung. Kann das funktionieren?
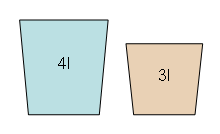
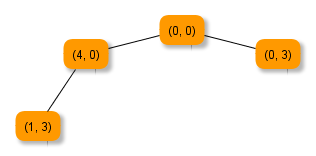
Um systematisch alle durch Umfüllen erzeugbaren Wassermengen zu bestimmen, kann man einen Zustandsgraphen erstellen. Die Knoten des Graphen sind die aktuellen Füllinhalte der beiden Eimer. Die Kanten des Graphen stellen die Umfüllvorgänge dar.
Aufgabe 1
Entwickle ein geeignetes Logikprogramm zur Lösung des Umfüllproblems. Die folgende Wissensbasis zeigt einen Weg auf, wie man die Umfüllvorgänge modellieren kann. Es fehlen aber noch eine Reihe von Regeln.
% Graph kante(X, Y) :- zustandsuebergang(X, Y). % 3-l-Eimer füllen zustandsuebergang((Eimer4, Eimer3), (Eimer4, 3)) :- Eimer3 \== 3. % 4-l-Eimer füllen ... % 3-l-Eimer leeren zustandsuebergang((Eimer4, Eimer3), (Eimer4, 0)) :- Eimer3 \== 0. % 4-l-Eimer leeren ... % 3-l-Eimer umfüllen in 4-l-Eimer zustandsuebergang((Eimer4, Eimer3), (Eimer41, 0)) :- Eimer3 \== 0, Eimer3 + Eimer4 =< 4, Eimer41 is Eimer3+Eimer4. % 4-l-Eimer umfüllen in 3-l-Eimer ... % 4-l-Eimer teilw. umfüllen in 3-l-Eimer ... % 3-l-Eimer teilw. umfüllen in 3-l-Eimer zustandsuebergang((Eimer4, Eimer3), (4, Eimer31)) :- Eimer4 \== 4, Eimer3 + Eimer4 >4, Eimer31 is Eimer3+Eimer4-4. % Ausgabe eines Weges ausgeben([]). ausgeben([K|R]) :- print(K), nl, ausgeben(R). % Start-/Zielzustand startZustand([0,0]). zielZustand([2,N]). zielZustand([M,2]). % Wegsuche weg2(X, X, W, W). weg2(X, Y, A, W) :- kante(X, Z), not(member(Z, A)), weg2(Z, Y, [Z|A], W). weg(W) :- startZustand(X), zielZustand(Y), weg2(X, Y, [X], W), ausgeben(W).