Wissensmodellierung mit Regeln
Explizite Beschreibung von Wissen
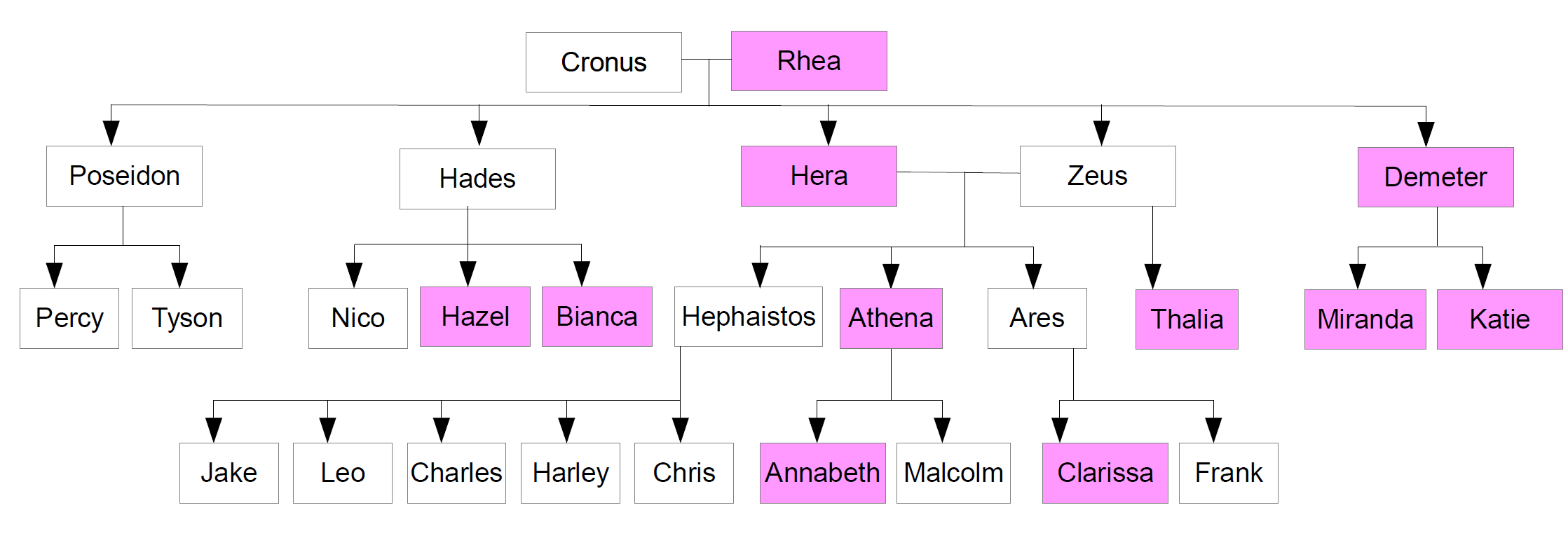
Wir betrachten weiterhin den Stammbaum der Halbgötter:
% Fakten
maennlich(cronus).
maennlich(zeus).
maennlich(poseidon).
maennlich(hades).
maennlich(ares).
maennlich(hephaistos).
maennlich(percy).
maennlich(tyson).
maennlich(nico).
maennlich(malcolm).
maennlich(frank).
maennlich(jake).
maennlich(leo).
maennlich(charles).
maennlich(harley).
maennlich(chris).
weiblich(rhea).
weiblich(hera).
weiblich(demeter).
weiblich(athena).
weiblich(hazel).
weiblich(bianca).
weiblich(miranda).
weiblich(katie).
weiblich(annabeth).
weiblich(clarissa).
weiblich(thalia).
kind(hera,cronus).
kind(hera,rhea).
kind(zeus,cronus).
kind(zeus,rhea).
kind(poseidon,cronus).
kind(poseidon,rhea).
kind(hades,cronus).
kind(hades,rhea).
kind(demeter,cronus).
kind(demeter,rhea).
kind(athena,zeus).
kind(athena,hera).
kind(ares,zeus).
kind(ares,hera).
kind(hephaistos,zeus).
kind(hephaistos,hera).
kind(percy,poseidon).
kind(tyson,poseidon).
kind(nico,hades).
kind(hazel,hades).
kind(bianca,hades).
kind(miranda,demeter).
kind(katie,demeter).
kind(annabeth,athena).
kind(malcolm,athena).
kind(clarissa,ares).
kind(frank,ares).
kind(jake,hephaistos).
kind(leo,hephaistos).
kind(charles,hephaistos).
kind(harley,hephaistos).
kind(chris,hephaistos).
kind(thalia,zeus).
In Kapitel 2 "Wissensmodellierung mit Fakten" habt ihr die Wissensbasis um das Prädikat mutter/2 erweitert.
mutter(rhea,hera).
mutter(hera,hephaistos).
mutter(hera,athena).
mutter(hera,ares).
mutter(demeter,miranda).
mutter(demeter,katie).
mutter(athena,annabeth).
mutter(athena,malcolm).
Auf diese Weise könnte man den Stammbaum auch durch das Prädikat vater/2, oma/2 und viele mehr erweitern.
Man würde das Wissen explizit mit Hilfe von Fakten in die Wissensbasis eintragen.
Aufgabe 1
a) Nenne Vorteile dafür, dass das Prädikat mutter/2 explizit in die Wissensbasis eingetragen wird.
b) Nenne Nachteile, wieso es ungünstig sein kann ein Prädikat explizit in die Wissensbasis einzutragen.
Implizite Beschreibung durch Wenn-Dann-Aussagen
Geschickter und schneller wäre es, wenn man Wissen auch implizit beschreiben könnte.
In der Miniwelt gilt z.B. die folgende Wenn-Dann-Aussage:
"[Alice ist Mutter von Bob] wenn [Bob Kind von Alice ist] und [Alice weiblich ist]."
Zur Erfassung impliziten Wissens durch solche Wenn-Dann-Aussagen erweitert man eine Wissensbasis
um sogenannte Regeln:
% Fakten
maennlich(cronus).
maennlich(zeus).
maennlich(poseidon).
maennlich(hades).
maennlich(ares).
maennlich(hephaistos).
maennlich(percy).
maennlich(tyson).
maennlich(nico).
maennlich(malcolm).
maennlich(frank).
maennlich(jake).
maennlich(leo).
maennlich(charles).
maennlich(harley).
maennlich(chris).
weiblich(rhea).
weiblich(hera).
weiblich(demeter).
weiblich(athena).
weiblich(hazel).
weiblich(bianca).
weiblich(miranda).
weiblich(katie).
weiblich(annabeth).
weiblich(clarissa).
weiblich(thalia).
kind(hera,cronus).
kind(hera,rhea).
kind(zeus,cronus).
kind(zeus,rhea).
kind(poseidon,cronus).
kind(poseidon,rhea).
kind(hades,cronus).
kind(hades,rhea).
kind(demeter,cronus).
kind(demeter,rhea).
kind(athena,zeus).
kind(athena,hera).
kind(ares,zeus).
kind(ares,hera).
kind(hephaistos,zeus).
kind(hephaistos,hera).
kind(percy,poseidon).
kind(tyson,poseidon).
kind(nico,hades).
kind(hazel,hades).
kind(bianca,hades).
kind(miranda,demeter).
kind(katie,demeter).
kind(annabeth,athena).
kind(malcolm,athena).
kind(clarissa,ares).
kind(frank,ares).
kind(jake,hephaistos).
kind(leo,hephaistos).
kind(charles,hephaistos).
kind(harley,hephaistos).
kind(chris,hephaistos).
kind(thalia,zeus).
% Regeln
mutter(MUTTER, KIND) :- kind(KIND, MUTTER), weiblich(MUTTER).
Beachte, dass der Regelkopf das neue Prädikat (hier: mutter/2) beschreibt. Das Symbol ":-" trennt den Regelkopf vom Regelrumpf, in dem
alle Bedingungen durch "," (logisches UND) verknüpft werden. Auch eine Regel muss immer mit einem Punkt abgeschlossen werden.
Sind bei einer Anfrage alle Bedingungen des Regelrumpfes erfüllt, liefert der Prolog-Interpreter bei einer Ja-Nein-Anfrage true. als Ergebnis.
Bei einer Ergänzungsanfrage gibt der Interpreter nur Belegungen aus, bei denen alle Bedingungen des Regelrumpfes erfüllt sind.
Aufgabe 2
Teste das angegebene Programm mit der neuen Regel für das Prädikat mutter/2. Verwende die Regel zum Abfragen folgender Informationen:
a) Ist Rhea die Mutter von Hera? Ist Katie die Mutter von Demeter und ist Hephaistos die Mutter von Harley?
b) Wer ist die Mutter von Malcolm?
c) Von wem ist Hera die Mutter?
Mehrere Regeln für ein Prädikat
Beachte, dass ein Prädikat auch mit mehreren Regeln festgelegt werden kann. Außerdem können Prädikate als Bedingung verwendet werden, die selbst durch eine
Regel neu geschaffen wurden (z.B. mutter/2).
tochter(KIND, PERSON) :- weiblich(KIND), mutter(PERSON, KIND).
tochter(KIND, PERSON) :- weiblich(KIND), vater(PERSON, KIND).
Logisch bedeutet das: Ein Kind ist Tochter einer Person, wenn das Kind weiblich ist und die Person Mutter des Kindes ist, oder wenn das Kind weiblich ist und die Person Vater des Kindes ist.
Tatsächlich könnte man beide Regelrümpfe auch in einer Regel mit einem ";" (logisches ODER) und passender Klammersetzung verknüpfen.
Aufgabe 3
Vervollständige die Regeln, überprüfe sie mit geeigneten Anfragen und beschreibe jede Regel mit einer geeigneten Wenn-Dann-Aussage.
vater(VATER,KIND) :-
elternteil(ELTERNTEIL, KIND) :-
sohn(SOHN, ELTERNTEIL) :-
oma(OMA, KIND) :-
Aufgabe 4
Warum muss man in der folgenden Regel die Bedingung BRUDER \== PERSON (für BRUDER und PERSON sind ungleich)
mit aufnehmen?
Tipp: Teste die Regel ohne die Bedingung.
bruder(BRUDER, PERSON) :- maennlich(BRUDER), elternteil(ELTER, BRUDER), elternteil(ELTER, PERSON), BRUDER \== PERSON.
Quellen
- [1]: Stammbaum der Halbgötter - Urheber: MB - Lizenz: inf-schule.de