Die Datenstruktur Binärbaum
Womit fangen wir an?
Alle Datenstrukturen, die wir bisher kennen gelernt haben, brauchten zu Beginn einen (im Fall unserer Listen) oder mehrere (im Falle unseres Arrays) Zeiger auf irgendwelche Blöcke im Speicher.
Es ist daher wohl gerechtfertigt anzunehmen, dass wir so etwas auch in unserer neuen Datenstruktur (nennen wir sie doch einfach Binärbaum ;)) benötigen.
In unserer binären Suche (für die der Binärbaum ja optimiert werden soll) benötigen wir zu Beginn immer genau ein Element, den Median unserer Liste. Daher werden wir unserem Binärbaum zunächst auch mal genau dieses eine Element mitgeben. Er sieht also in dem Fall ziemlich simpel aus:
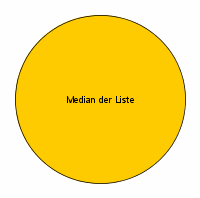
Hier unterscheidet sich der Binärbaum natürlich noch nicht von einer Liste, aber er besteht ja bisher auch nur aus einem Element. Da wir ja vorher nicht zwingend wissen, wie groß unsere Datenmenge ist und sie daher ja auch aus nur einem Element bestehen kann, ist obiges ja schon ein Binärbaum.
Womit machen wir weiter?
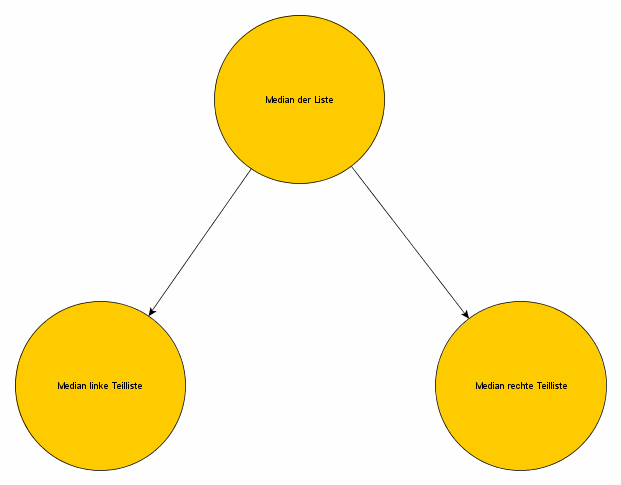
Unser binäre Suche Algorithmus vergleicht im ersten Schritt das gesuchte Element mit dem Median (also unserem ersten Baumelement), gibt es wieder, wenn sie übereinstimmen, geht zum Median der linken Teilliste, wenn das gefundene Element größer als das gesuchte ist und zum Median der rechten Teilliste, wenn das gefundene Element kleiner als das gesuchte ist.
Wir brauchen also genau zwei Zeiger von unserem ersten Element (welches wir fortan entsprechend dem Baumnamen Wurzel nennen wollen), einen auf den Median der linken Teilliste (der kleiner als die Wurzel ist) und einen auf den Median der rechten Teilliste (der größer als die Wurzel ist):
Und dann?
Da wir unseren Algorithmus rekursiv definiert haben, werden wir immer nur für jedes Element (wir wollen es zukünftig mal Knoten nennen) zwei Zeiger auf die nächsten zwei Mediane brauchen, bis wir schließlich bei den untersten Elementen (die wir wieder entsprechend unserer Baumanalogie Blätter nennen wollen) ankommen.
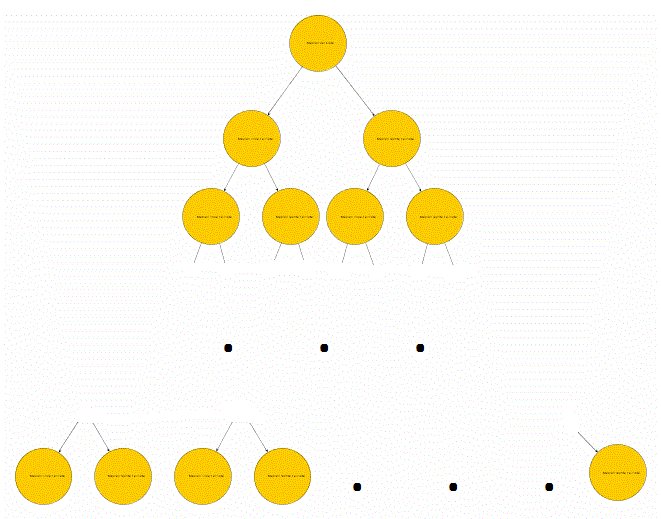
Wir haben also für jedes Element genau zwei Zeiger, sehen also auch schon, dass der Speicherbedarf unseres Baumes dem der doppelt verketteten Liste entspricht.
Aufgabe 1
(a) Baue so den Baum, der sich aus der Liste 1, 5, 9, 11, 23, 47, 55, 56, 99 ergibt auf.
(b) Wieviele Vergleiche brauchen wir bei der binären Suche nach 56 und 1 in diesem Baum?
(c) Wenn wir nun eine binäre Suche auf dem Binärbaum durchführen würden (also mal unter der Annahme, wir hätten ihn schon implementiert), wie viele Baumelemente müssen "abgelaufen" werden, mit denen wir nicht direkt einen Vergleich anstellen?
Eine formalere Definition
Wir wollen uns nun unseren Binärbaum etwas genauer definieren. Dabei müssen wir beachten, dass es vielleicht noch viel mehr Anwendungsmöglichkeiten für unsere Bäume gibt, als nur die binäre Suche.
Wir können unseren Binärbaum also nicht anhand des Medians einer Liste definieren. Dennoch werden wir eine Möglichkeit haben, unseren Binärbaum auf einen solchen Fall einzuschränken.
- Ein Binärbaum besteht aus einer Wurzel und einer endlichen Anzahl an Knoten.
- Jeder Knoten A eines Binärbaums(inklusive der Wurzel) hat null, ein oder zwei Zeiger auf weitere Knoten. Diese Knoten bezeichnen wir als die Kinder des Knotens A, genauer als linkes und rechtes Kind des Knotens A.
- Hat ein Knoten A ein linkes Kind L, so ist L kleiner oder gleich A und alle Kinder von L sind auch kleiner oder gleich A. Hat ein Knoten A ein rechtes Kind R, so ist R größer als A und alle Kinder von R sind auch größer als A. A bezeichnen wir auch als Vater von L, bzw. R (das kleiner gleich und echt größer ist zu Zwecken der Eindeutigkeit gewählt und hat keinen inhaltlichen Grund).
- Jeder Knoten (außer der Wurzel) hat genau einen Vater.
Alternativ können wir einen Binärbaum auch mit Hilfe der Graphentheorie beschreiben:
Wir sehen also, dass unser Binärbaum "nur" ein sehr spezieller Graph ist. Wenn Du also schon etwas über Graphen weißt, kannst Du dein Wissen hier benutzen!
Es gibt auch noch eine sehr schöne, weil besonders einfache Definition:
Ein einzelner Knoten ist ein Binärbaum.
Sind A und B Binärbäume und sind alle Knoten in A kleiner oder gleich dem Knoten R, sowie alle Knoten in B größer als der Knoten R so ist auch
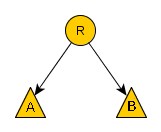
Du musst nicht all diese Definitionen verstehen, um weiterzumachen. Es reicht völlig, wenn Du nur die erste Definition verstanden hast. Die anderen Definitionen sind nur da, damit Leute, die Graphen kennen den Zusammenhang sehen und aufgrund der schönen Schlichtheit der zweiten Definition.
Zum Abschluss unserer Definition wollen wir noch ein paar Begriffe zum Binärbaum definieren:
- Hat ein Knoten A keine Kinder, so nennen wir A ein Blatt (ja: Die Wurzel kann glechzeitig auch ein Blatt sein!).
- Wir bezeichnen die Anzahl der Kanten zwischen einem Knoten A und der Wurzel als die Höhe des Knotens A.
- Wir bezeichnen einen Binärbaum B als höhenbalanciert, wenn die Höhe zweier beliebiger Blätter in B sich um nicht mehr als 1 unterscheidet.
Aufgabe 2
(a) Betrachten wir deinen in Aufgabe 1 erstellten Baum, er könnte in etwa so aussehen:
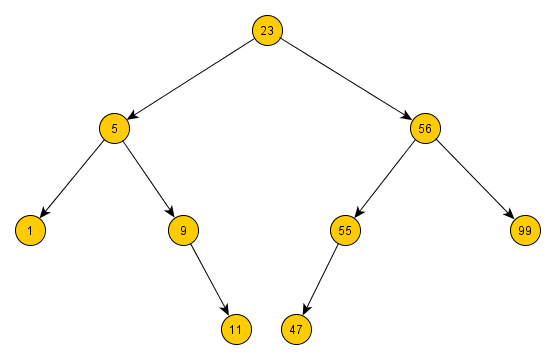 Erfüllt dieser unsere Definition
des Binärbaums?
Erfüllt dieser unsere Definition
des Binärbaums?
(b) Erstelle einen höhenbalancierten Binärbaum mit den Knoten 1, 5, 9, 11, 23, 47, 55, 56, 99 und vergleiche ihn mit deinem in Aufgabe 1 erstellten Baum. Gibt es auch andere höhenbalancierte Binärbäume mit diesen Knoten? Wenn ja, welche? Wenn nein, warum nicht?
(c) Erstelle einen höhenbalancierten Binärbaum mit den Knoten 1, 5, 9, 11, 23, 47, 55, 56, 99, 100. Gibt es auch andere höhenbalancierte Binärbäume mit diesen Knoten? Wenn ja, welche? Wenn nein, warum nicht?
(d) Gibt es eine allgemeine Regel, wie viele höhenbalancierte Binärbäume es gibt in Abhängigkeit von der Knotenzahl? Wenn ja, wie sieht sie aus?
(e) Sind die Bäume, die wir erstellen, wenn wir nach obigem Verfahren vorgehen höhenbalanciert? Was ist der Zusammenhang zwischen unseren Bäumen von oben und höhenbalancierten Bäumen?
(f) Zusatzaufgabe: Warum sind die erste und letzte Definition für Binärbäume gleich?
(g) Zusatzaufgabe, wenn Du Graphen kennst: Warum sind die erste und zweite Definition für Binärbäume gleich?
(h) Zusatzaufgabe, wenn du Induktion kennst und viel Lust hast: Beweise deine Aussage (d). Tipp: Benutze die dritte Definition des Binärbaums.