Lösung des Problems
Graphen mit Kreisen
Wir betrachten jetzt die Wegsuche in beliebigen gerichteten Graphen - die also auch Kreise enthalten können.
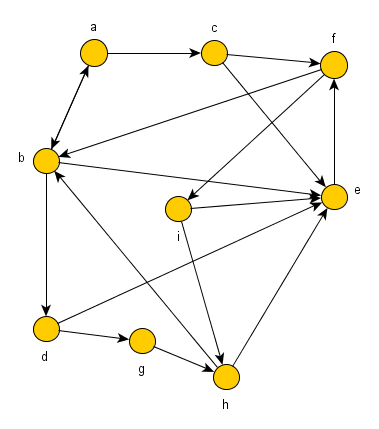
Beachte, dass jetzt weitere Fakten in die Wissensbasis übernommen werden müssen.
% Graph kante(a, b). kante(a, c). kante(b, d). kante(b, e). kante(c, e). kante(c, f). kante(d, g). kante(d, e). kante(f, b). kante(f, i). kante(h, e). kante(h, b). kante(i, e). kante(i, h). % Weg weg2(X, X, W, W). weg2(X, Y, A, W) :- kante(X, Z), not(member(Z, A)), weg2(Z, Y, [Z|A], W). weg(X, Y, W) :- weg2(X, Y, [X], W).
Die folgenden Regeln zur Festlegung eines weg2-Prädikats benutzen eine zusätzliche
Bedingung not(member(Z, A)). Wenn diese Bedingung bei der Auswertung von Fakten
nicht erfüllt ist, wird ein Herleitungsversuch abgebrochen.
Aufgabe 1
Teste das weg-Prädikat mit geeigneten Anfragen.
?- weg(a, b, W). ...
Überprüfe die Korrektheit der Ergebnisse.