Lösung eines vereinfachten Problems
Vereinfachung des Graphenproblems
Zur Vereinfachung des Graphenproblems betrachten wir vorerst nur Graphen, die keine Kreise enthalten.
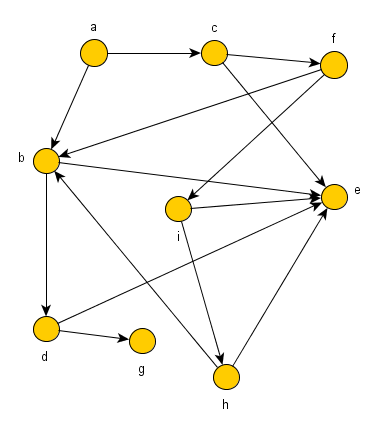
Zunächst soll es nur darum gehen, die Existenz von Wegen zwischen Knoten des Graphen zu überprüfen.
Beschreibung des Graphen
Zur Beschreibung der Knoten des Graphen werden entsprechende Konstanten eingeführt.
Die Kanten des Graphen werden mit Hilfe eines Prädikats kante/2 erfasst.
Für jede Kante wird ein entsprechendes Faktum in der Wissensbasis aufgenommen.
% Graph kante(a, b). kante(a, c). kante(b, d). kante(b, e). kante(c, e). kante(c, f). kante(d, g). kante(d, e). kante(f, b). kante(f, i). kante(h, e). kante(h, b). kante(i, e). kante(i, h).
Wege in einem so beschriebenen Graphen sollen mit dem Prädikat weg/2 erfasst werden.
Eine deklarative Beschreibung dieses Prädikats kann von folgenden Regeln ausgehen:
Regel 1: Es gibt einen Weg zwischen einem Knoten X und einem Knoten Y, wenn es eine Kante von X nach Y gibt. Regel 2: Es gibt einen Weg zwischen einem Knoten X und einem Knoten Y, wenn es eine Kante von X zu einem Knoten Z und einen Weg vom Knoten Z zum Knoten Y gibt.
Aufgabe 1
Entwickle geeignete Prolog-Regeln zur Festlegung des weg-Prädikats.
Teste die entwickelten Regeln mit Anfragen wie der folgenden.
% Anfrage ?- weg(a, h).

