Exkurs - Tiefensuche
Wegsuche mit Ausgaben
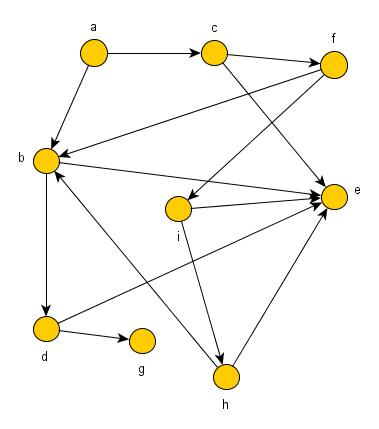
Wir betrachten weiterhin die Wegsuche in gerichteten Graphen ohne Kreise und verdeutlichen die Ergebnisse am folgenden Beispielgraphen.
Die folgenden Regeln zur Festlegung des weg-Prädikats benutzen ein zusätzliches
print-Prädikat, mit dem während der Auswertung von Anfragen Ausgaben auf dem Bildschirm
erzeugt werden können.
% Graph kante(a, b). kante(a, c). kante(b, d). kante(b, e). kante(c, e). kante(c, f). kante(d, g). kante(d, e). kante(f, b). kante(f, i). kante(h, e). kante(h, b). kante(i, e). kante(i, h). % Weg weg(X, Y) :- kante(X, Y), print(Y). weg(X, Y) :- kante(X, Z), print(Z), weg(Z, Y).
Aufgabe 1
(a) Teste zunächst die Regeln mit Anfragen wie der folgenden.
?- weg(a, h). bdgeecefbdgeeih Yes
Kannst du erklären, wie die Ausgaben zu Stande kommen?
(b) Warum bezeichnet man die Suche hier auch als "Tiefensuche"?
Aufgabe 2
Kann man auch das mit den unten gezeigten Regeln festgelegte weg-Prädikat benutzen,
um festzustellen, ob es einen Weg von einem Startknoten X zu einem Zielknoten Y in einem
vorgegebenen Graphen ohne Kreise gibt?
% Weg weg(X, X). weg(X, Y) :- kante(X, Z), weg(Z, Y).
Teste dieses weg-Prädikat und erkläre die Arbeitsweise.
Aufgabe 3
Warum funktioniert die Tiefensuche mit dem bisher festgelegten weg-Prädikat
nicht bei Graphen mit Kreisen? Probiere es ggf. aus, indem du eine zusätzliche Kante im
Graphen einführst.