Kara als Taschenrechner
Kara lernt rechnen
Du hast bereits festgestellt, dass man in Python mit Variablen rechnen kann, z.B. durch Zuweisungen wie anzahl2 = anzahl1*3.
Durch die Verwendung von Unterprogrammen mit Rückgabewert haben wir nun einen einfachen Weg, um Anzahlen aus unserer Kara-Welt auszulesen (z.B. die Länge von Blattreihen).
Dann können wir mit Python rechnen. Und durch Unterprogramme mit Parametern können wir die brechneten Werte auch einfach wieder (z.B. als Blattreihe) auf der Welt abbilden.
Diesen Vorgang möchten wir hier umsetzen.
Aufgabe
Wir möchten zwei Unterprogramme verwenden, um einen „Taschenrechner“ zu programmieren.
Die eigentlichen Rechnung macht dabei in der Regel Python mit
+, -, * und /.
Wir können aber eine schöne Ausgabe dafür programmieren.
# Unterprogramme
def countLeafs():
i = 0
while kara.onLeaf():
kara.move()
i = i+1
return i
def walkAndPut(distance):
i = 0
while i < distance:
kara.putLeaf()
kara.move()
i = i+1
# Hauptprogramm
...
(a) Schreibe ein kurzes Hauptprogramm für einen Additionsrechner. Man soll in der Kara-Welt zwei Summanden durch Blattreihen darstellen (z.B. 3+2 im nachfolgenden Beispiel).
Kara soll die Längen der Reihen zählen (und mit zwei Variablen speichern), dann die Summe berechnen (mit +) und in der Zeile darunter
eine entsprechende Blattreihe auslegen.
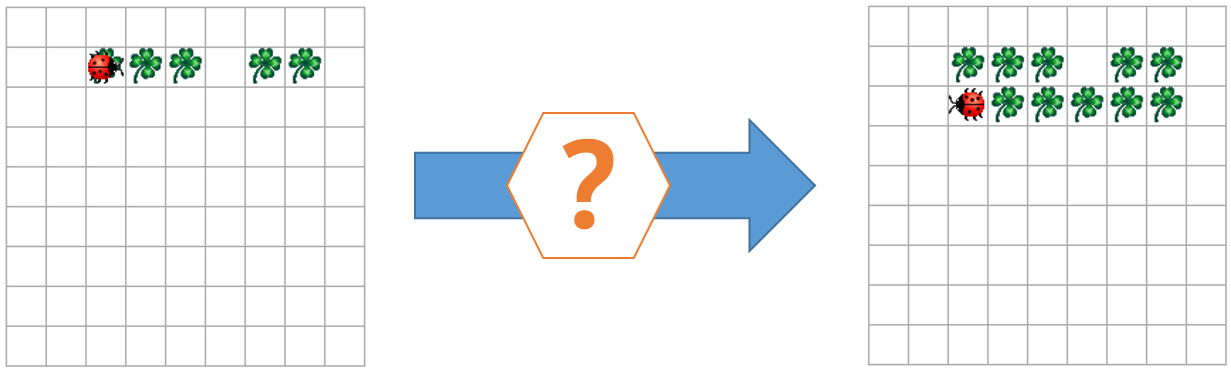
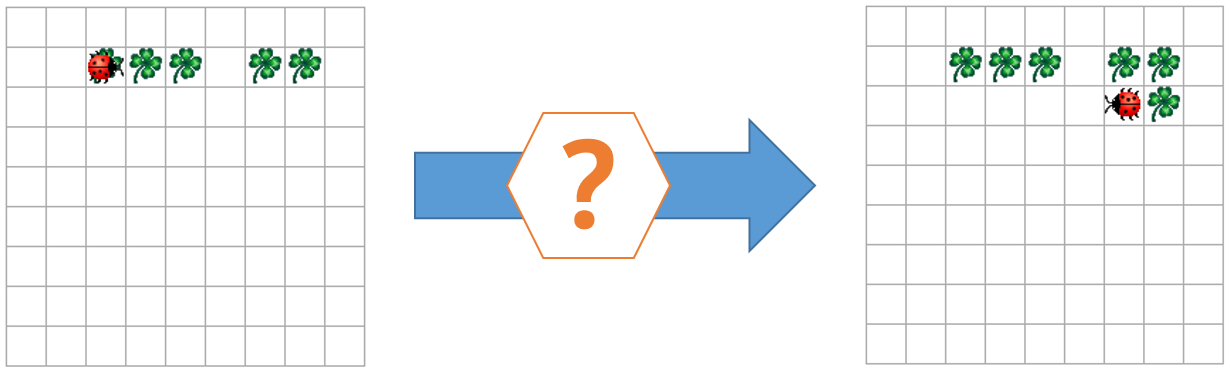
(b) Schreibe analog zu Teil (a) ein Programm für die Subtraktion.
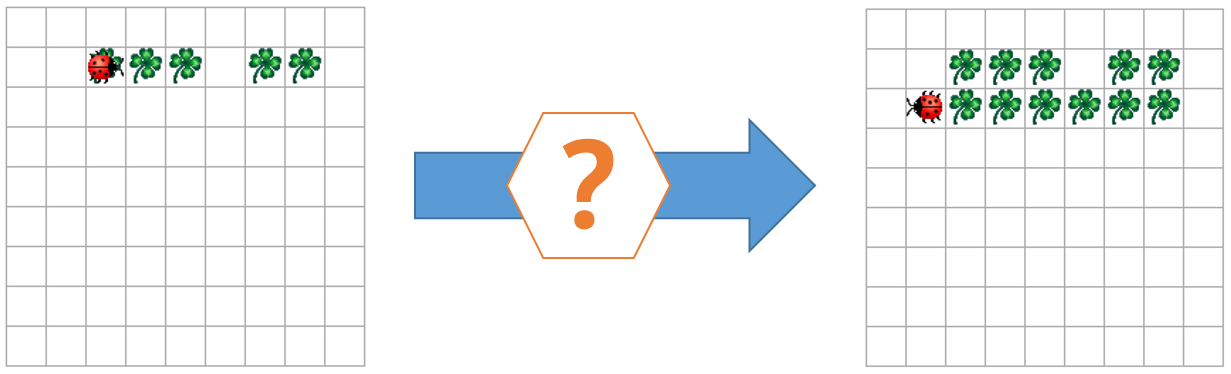
(c) Schreibe analog zu Teil (a) und (b) ein Programm für die Multiplikation.
(d) Schreibe analog zu Teil (a) und (b) ein Programm für die Division. Betrachte dabei, was der Befehl / genau macht, wenn die Rechnung kein ganzzahliges Ergebnis liefert.
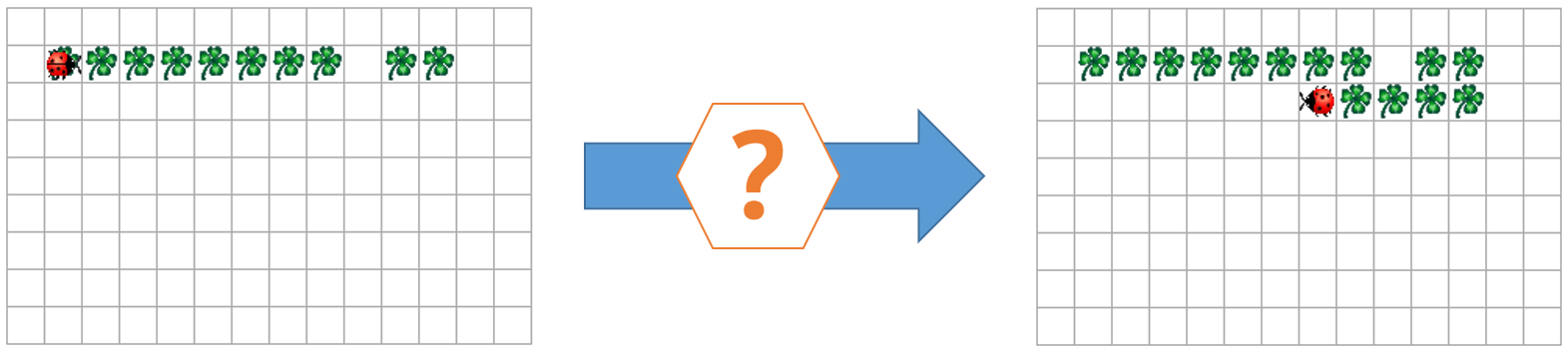
(e) Optional: Die eigentlichen Rechnungen waren nun sehr einfach: Schließlich haben wir die entsprechenden Python-Operationen verwendet. Es gäbe so eine Operation auch für z.B. die Potenz. Wir wissen aber nicht, wie wir das genau schreiben müssen. Du kannst das Problem aber lösen: Eine Potenz ist eine wiederholt durchgeführte Multiplikation. Mit einer Schleife und dem *-Operator, solltest du also auch Potenzen berechnen können. Probiere das aus. Die Potenz $2^3=8$ siehst du im folgenden Bild:
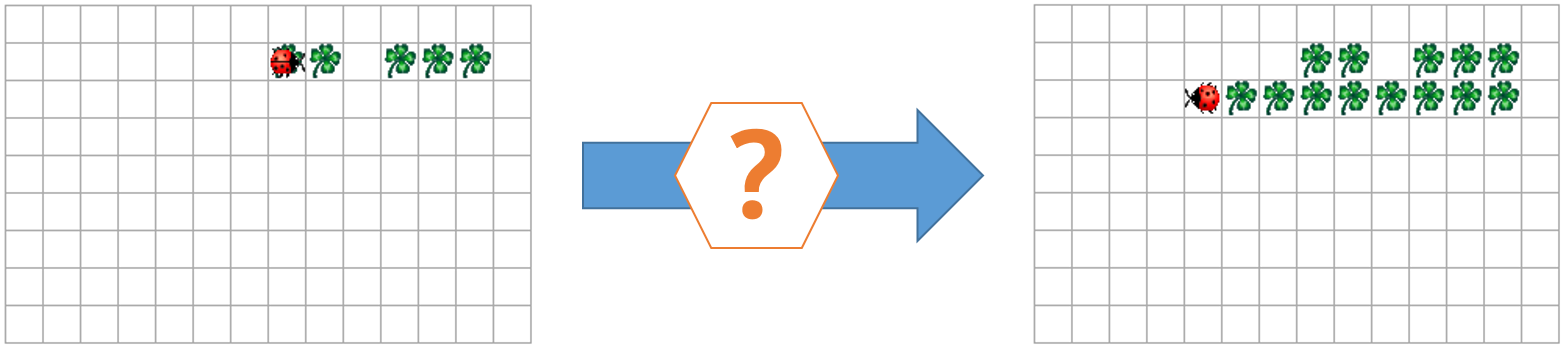
Für die Rechnung $b^n$ möchtest du die Basis $b$ genau $n$ mal mit sich selbst multiplizieren. Du kannst nun mit einer Variable potenz starten, der du den Wert 1 zuweist. Nun soll in einer Schleife immer die Potenz mit der Basis multipliziert werden. Das geht so:potenz = potenz * basis. Wie oft die Schleife ausgeführt wird, regelt die Variable exponent. Dafür kannst du den Wert dieser Variable einfach in jedem Durchlauf der Schleife um 1 verringern, bis er 0 beträgt.
(f) Optional: Der Zusammenhang aus Teil (e) wird kurz so beschrieben: „Eine Potenz ist eine iterierte (also wiederholt ausgeführte) Multiplikation.“ Genauso gilt aber auch: Eine Multiplikation ist eine iterierte Addition (einfach) und eine Division ist eine iterierte Subtraktion (schwieriger). Versuche deine Programme aus den Aufgabenteilen (c) und (d) so anzupassen, dass du die Python-Operatoren * und / nicht mehr benötigst.
Hintergrund der Aufgaben (e) und (f)
Man kann die Aufgabenteile (e) und (f) einfach als eine kleine Programmierübung betrachten. Es gibt jedoch auch einen informatischen Hintergrund dazu. Eine wichtige Frage im zwanzigsten Jahrhundert war es, mit welchen Grundoperationen man einen Computer aufbauen kann. Kurz gesagt: Was muss eine Maschine eigentlich können, damit sie das kann, was wir von einem Computer erwarten.
Um z.B. beweisen zu können, welche Probleme man mit Computern algorithmisch lösen kann und (vor allem) welche nicht, war es sinnvoll, sich ein möglichst einfaches Modell auszudenken. Dabei muss man dann aber zeigen, dass ein einfaches Modell (z.B. eines, in dem die Operatoren * und / nicht vorhanden sind) dennoch in der Lage ist, komplizierte Probleme zu lösen. Im Kleinen hast du genau das in den beiden Aufgabenteilen gemacht: Du hast drei Operationen (Potenz, Multiplikaiton, Division) auf grundlegendere Operationen zurückgeführt. Ein Computer, der Schleifen und Addition beherrscht, kann somit auch multiplizieren und potenzieren.
Eine intensivere Betrachtung solcher Fragestellungen findet im Kapitel zur Berechenbarkeit statt.