Perzeptron als künstliches Neuron
Als erstes Modell für eine künstliche Nervenzelle soll nun ein so genanntes Perzeptron definiert werden, mit dem die Gefährlichkeit von Tieren beurteilt werden kann. Als Eingabegrößen hat das Perzeptron die Zahngröße $x_1$ und die Augengröße $x_2$ des Tieres. Als Ausgabegröße kann das Perzeptron die binären Werte $y \in \{0,1\}$ annehmen:
\begin{eqnarray} y = \left\{\begin{array}{ll} 1 & \textrm{gefährlich} \\ 0 & \textrm{ungefährlich} \end{array}\right. \nonumber \end{eqnarray}Überschreiten die Eingabegrößen $x_1,x_2$ bestimmte Werte, so soll das Tier als gefährlich eingestuft werden, andernfalls als ungefährlich.
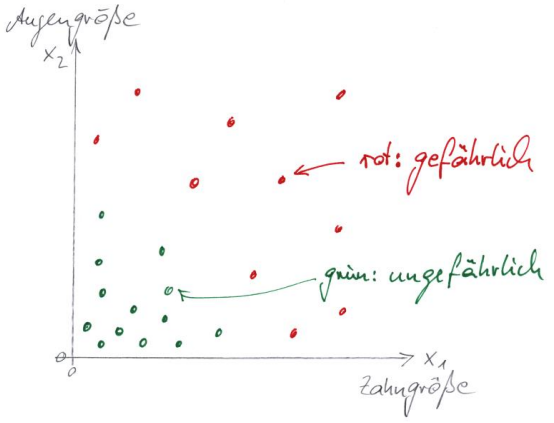
Die Abbildung veranschaulicht die Klassifikation von Tieren nach gefährlich und ungefährlich. Tiere mit großen Zähnen oder mit großen Augen werden als gefährlich eingestuft.
Um die Ausgabefunktion $y\in \{0,1\}$ genauer zu definieren, wird sie durch ein sogenanntes Perzeptron mit den beiden Eingängen $x_1,x_2 \in \mathbb{R}$ für die Zahn- und die Augengröße modelliert. Als konkrete Werte für die Klassifizierung von Tieren werden hier beispielhaft die Gewichte $w_1=1, w_2=0,5$ und der Schwellenwert $\Theta = 2$ gewählt:
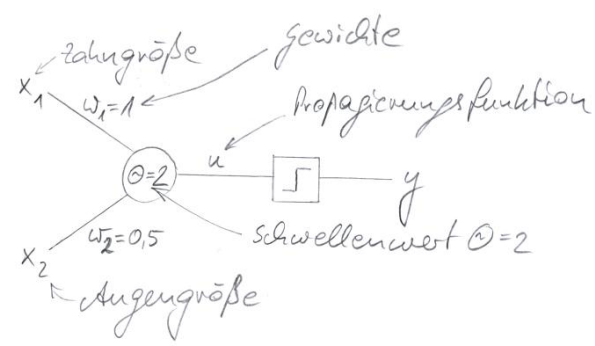
Durch die unterschiedliche Wahl der Gewichte wird bei der Beurteilung eines Tieres nach dessen Gefährlichkeit die Zahngröße hier also doppelt so stark gewichtet wie dessen Augengröße. Erst wenn die gewichtete Summe aus Zahn- und Augengröße den Schwellenwert von 2 überschreitet, feuert das Neuron und das Tier wird als gefährlich eingestuft.
Genauer wird die Ausgabefunktion $y \in \{0,1\}$ mit Hilfe der folgenden Zwischenschritte berechnet:- Zunächst wird der Wert der so genannten Propagierungsfunktion $u(x_1,x_2)$ als gewichtete Summe der beiden Eingangsgrößen $x_1,x_2$ bestimmt zu: \begin{eqnarray} u(x_1,x_2) &:=& w_1 \cdot x_1 + w_2 \cdot x_2 \nonumber \\ &=& 1 \cdot x_1 + 0,5 \cdot x_2 \nonumber \end{eqnarray}
- Nun wird als Aktivierungsfunktion des Perzeptrons die Treppenfunktion $f_2$ mit dem Schwellenwert (treshhold, bias) $\Theta=2$ gewählt, also: \begin{eqnarray} f_{2}(u) := \left\{\begin{array}{ll} 1 & u \ge 2 \\ 0 & u < 2\end{array}\right. \nonumber \end{eqnarray}
- Schließlich wird die Ausgangsfunktion y definiert als Verkettung von Propagierungs- und Aktivierungsfunktion: \begin{eqnarray} y(x_1,x_2) = f_{2} ( u(x_1,x_2 )) \nonumber \end{eqnarray}